Mischungstemperaturvorgaben parallel geschalteter Wärmeerzeuger unterschiedlichen Temperaturniveaus
In diesem Artikel wird beschrieben, wie in TOP-Energy ein Energiesystem mit zwei oder mehr parallel geschalteten Wärmeerzeugern mit unterschiedlichen Vorlauftemperaturen so simuliert wird, dass eine bestimmte Mischungstemperatur nicht unterschritten wird. Aufgrund der Besonderheiten der Wärme werden dazu in TOP-Energy Komponenten der Programmierbaren Steuerung verwendet.
Der Artikel richtet sich an erfahrene TOP-Energy-Anwender, da die komplexen Sachverhalte ein tiefgründiges Verständnis der Simulations- und Optimierungsvorgänge voraussetzen.
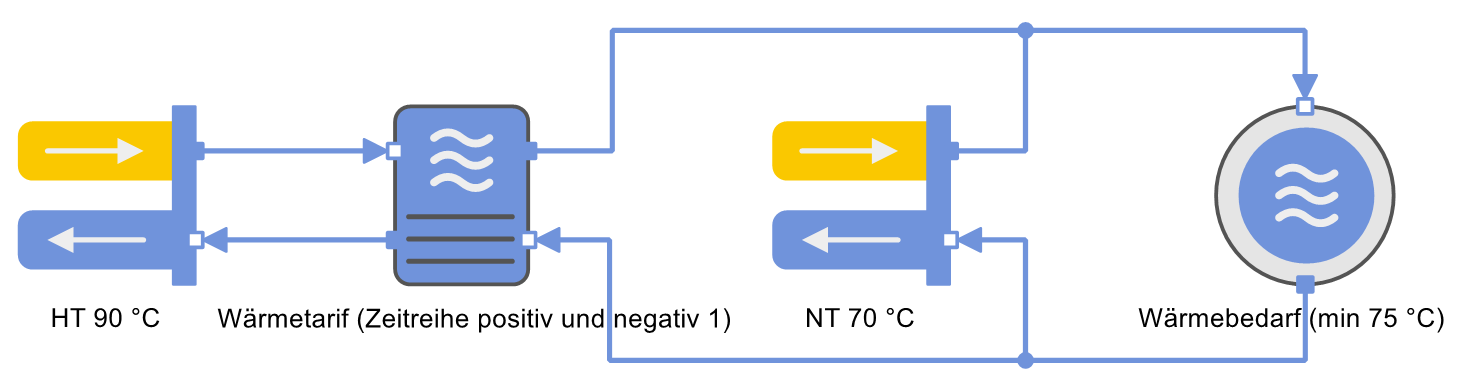
Das Energiesystem in der folgenden Abbildung verdeutlicht die Problemstellung.
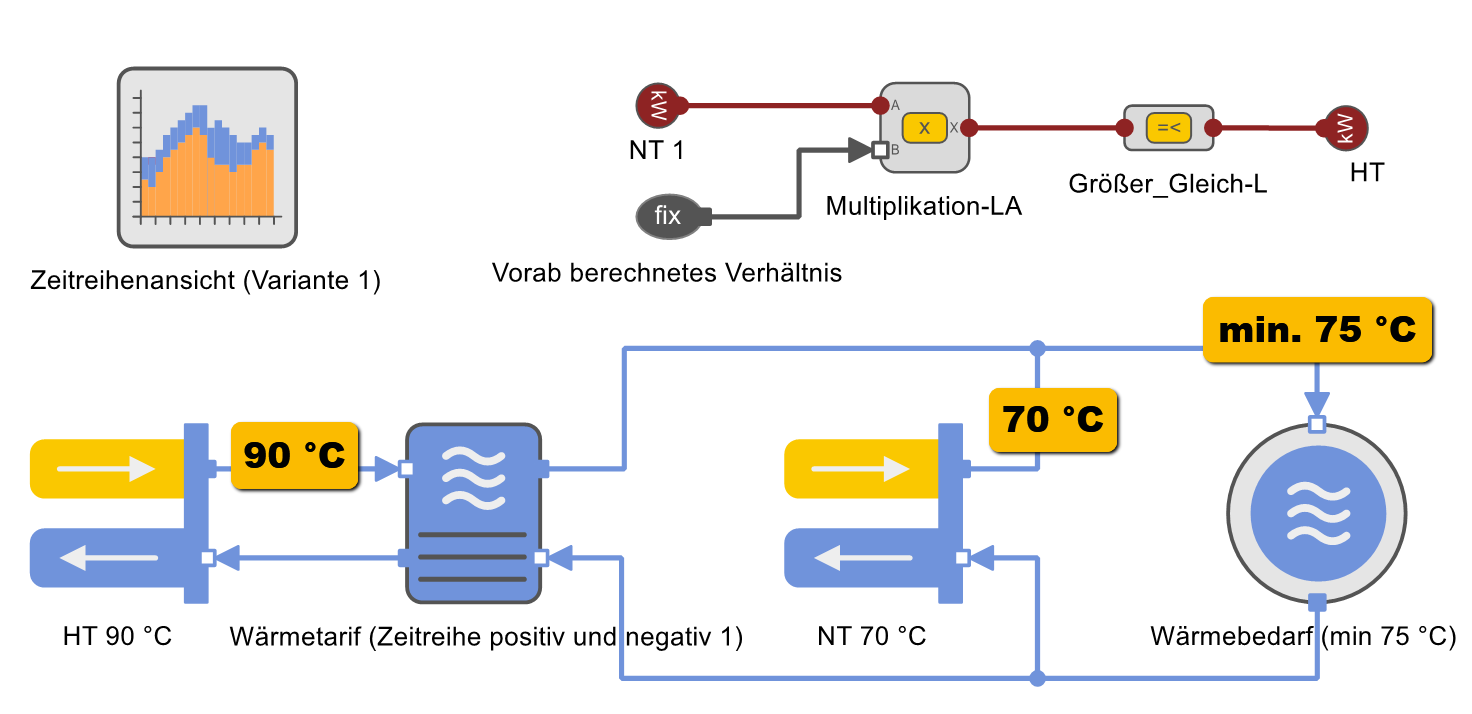
Durch die vorab bekannten Vorlauf- und Solltemperaturen wird das minimale Verhältnis der zu erzeugenden Wärmemengen mit Hoch- und Niedertemperatur berechnet. Dieses Verhältnis geht als lineare Schranke in das Optimierungsproblem ein.
Die Anwendung ist nicht auf Wärme beschränkt. Die Prinzipien lassen sich ebenso auf Kältenetze übertragen.
Ein ähnliches wie das hier vorgestellte Lösungsprinzip wird in dem Tutorial zu Wärmeerzeugern auf unterschiedlichen Temperaturniveaus für die Reihenschaltung vorgestellt. Auch wenn das Grundprinzip der Herleitung dasselbe ist, muss zwischen der Parallel- und der Reihenschaltung unterschieden werden.
Problembeschreibung am Beispiel
Ein Wärmebedarf mit einer minimalen Eintrittstemperatur von 75 °C soll durch zwei Wärmeerzeuger, einen Hochtemperaturwärmeerzeuger (HT) mit einer Vorlauftemperatur von 90 °C und einen Niedertemperaturwärmeerzeuger (NT) mit einer Vorlauftemperatur von 70 °C, gedeckt werden. Der Niedertemperaturwärmeerzeuger kann den Wärmebedarf nicht allein decken, weil damit die minimale Temperatur von 75 °C nicht erreicht wird. Da die Niedertemperaturwärme kostenlos und die Hochtemperaturwärme mit einem Preis versehen ist, gilt es, die optimale (kostengünstigste) Mischung zu berechnen.
In der Energiesystemoptimierung wird zur Vermeidung nichtlinearer Probleme die Mischungstemperatur nicht als Optimierungsvariable geführt, sondern durch eine untere Schranke für das Verhältnis der Nieder- und Hochtemperaturwärmemengen indirekt bestimmt. In TOP-Energy wird das Problem mithilfe der Steuerungskomponenten wie folgt gelöst:
Die graphischen Steuerungselemente geben die folgende Gleichung wieder:
\( \begin{equation} \begin{aligned} \dot{Q}_{HT} \ge c \cdot \dot{Q}_{NT} && \qquad(1)\\[.3cm] \end{aligned}\end{equation} \),
in der \( c \) eine Konstante darstellt, die in das Formular der als Vorab berechnetes Verhältnis benannten Komponente eingetragen wird. Die Rechenvorschrift folgt unten im Abschnitt Berechnung des Wärmeverhältnisses.
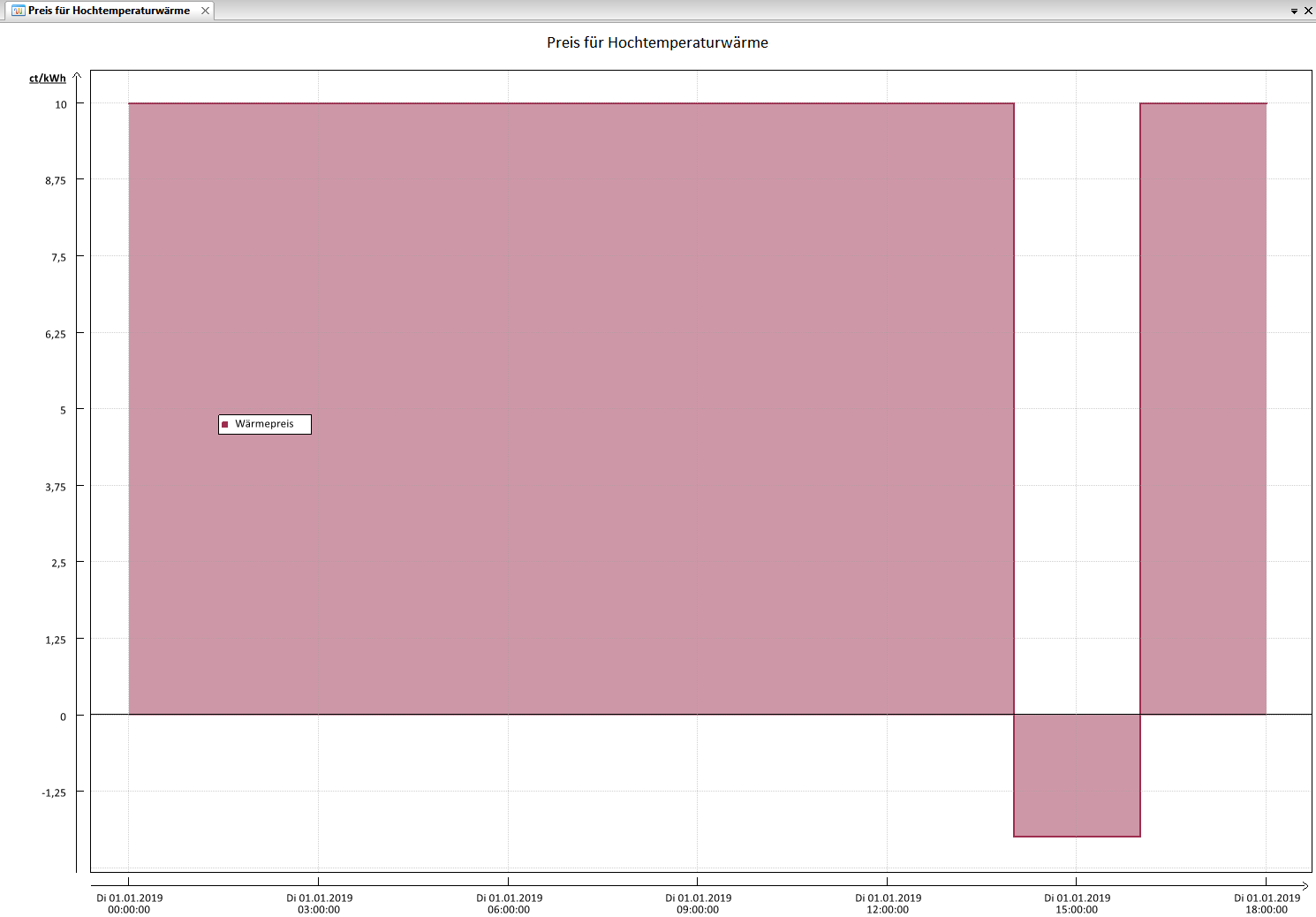
Im Tutorial wird als Eingabewert für den Preis der Hochtemperaturwärme (im Wärmetarif) die folgende Zeitreihe hinterlegt:
Der Wärmepreis ist im Simulationszeitraum von einigen Stunden konstant 9 ct/kWh, nur im vorletzten Zeitschritt hat er einen negativen Wert und wandelt sich damit in Erlös um.
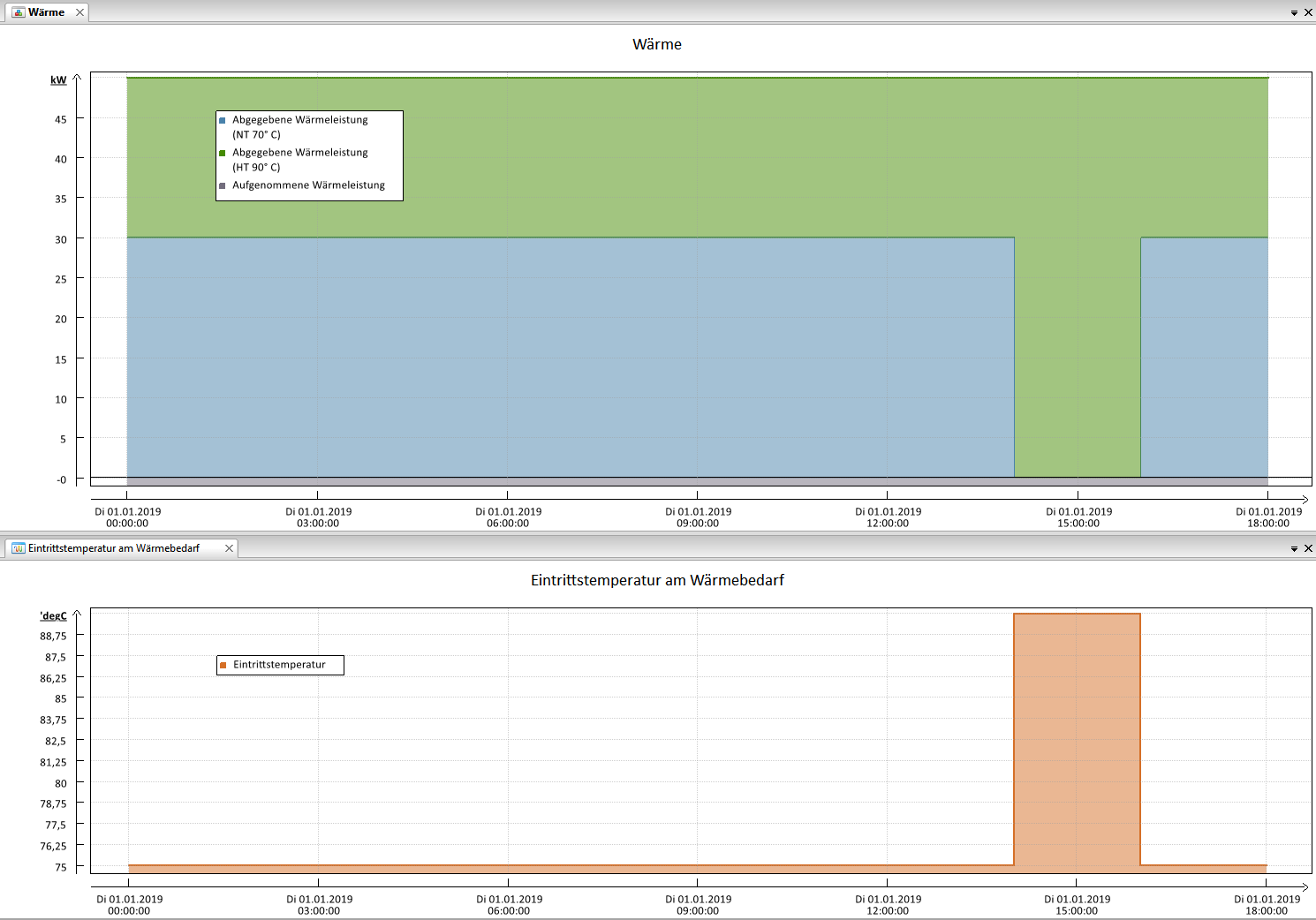
Die folgende Abbildung zeigt das optimierte Ergebnis der Simulation für die produzierte Wärme und die Eintrittstemperatur am Wärmebedarf.
Die Vorgabe, dass die Eintrittstemperatur am Wärmebedarf mindestens 75 °C beträgt, ist eingehalten.
Im Unterschied zum Normalfall eines positiven Wärmepreises, in dem nur so viel teure Hochtemperaturwärme verwendet wird, dass die vorgegebenen minimalen 75 °C erreicht werden, wird im Zeitschritt des negativen Wärmepreises ausschließlich Hochtemperaturwärme verwendet, weil durch den negativen Preis Erlöse erzielt werden und diese im Rahmen der Optimierung maximiert werden. Daher ist zu den Zeitpunkten des negativen Wärmepreises die Eintrittstemperatur am Wärmebedarf höher als 75 °C. Dies zeigt, dass TOP-Energy das Energiesystem auch im Rahmen der vorgegebenen Schranken, hier der minimalen Eintrittstemperatur von 75 °C, optimiert.
Berechnung des Wärmeverhältnisses
Wenn die Temperaturen der Erzeuger nicht konstant und deshalb mit einer Zeitreihe versehen sind, ist auch \( c \) keine über den Simulationszeitraum gleichbleibende Konstante. In diesem Fall ändert sich \( c \) mit den Temperaturverhältnissen. Man könnte zwar für \( c \) eine Zeitreihe vorab berechnen und vorgeben, aber deutlich flexibler ist die direkte temperaturabhängige Berechnung des Verhältnisses \( c \) in TOP-Energy.
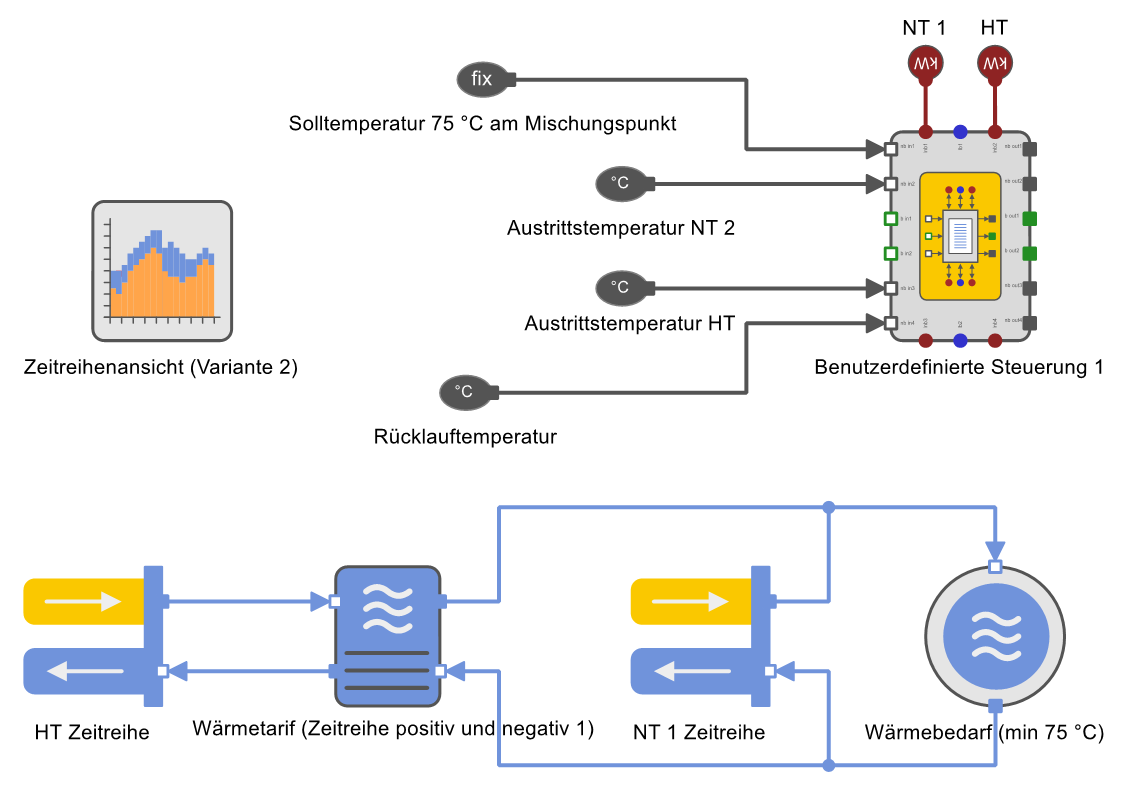
Beispielhaft zeigt die folgende Abbildung dafür dasselbe Modell mit einem Hoch- und einem Niedertemperaturwärmeerzeuger mit variierender Vorlauftemperatur.
Die beiden Wärmeerzeuger sind mit Zeitreihen für die variierenden Austrittstemperaturen versehen. Diese werden über die Komponenten Temperatur_Eingang-A (Temperaturfühler, siehe folgende Abbildung) ausgelesen.
In der Komponente Benutzerdefinierte Steuerung wird der Faktor \( c \), der das Wärmemengenverhältnis beschreibt, berechnet.
Es ist ebenso möglich, die Rechenoperationen durch die Steuerungselemente für Addition, Subtraktion, Multiplikation und Division +, –, * und / aus den Komponentenvorlagenordnern Programmierbare Steuerungen → Berechnungen darzustellen. Wegen der umfangreichen Rechenoperationen ist diese Methode nicht sehr übersichtlich. Daher wird stattdessen die Benutzerdefinierte Steuerung eingesetzt. In den Eingabedaten dieser Komponente sind im Fenster PML-Eingabe, das sich unter der Überschrift Steuerung befindet, die Rechenschritte einsehbar.
Der Anteil \( \alpha \) der jeweiligen Masse am Gesamtmassenstrom wird definiert. Die Massenbilanz am Mischungspunkt lautet:
\( \begin{equation} \begin{aligned} \dot{m}_{mix} &= \dot{m}_{HT} + \dot{m}_{NT} && \qquad(2),\\[.3cm] \dot{m}_{HT} &= \alpha \cdot \dot{m}_{mix} && \qquad(3),\\[.3cm] \dot{m}_{NT} &= (1-\alpha) \cdot \dot{m}_{mix} && \qquad(4).\\[.3cm] \\ \end{aligned}\end{equation} \)Die Energiebilanz lautet:
\(\\ \begin{equation} \begin{aligned} \dot{H}_{mix} &= \dot{H}_{HT} + \dot{H}_{NT} && \qquad(5),\\[.3cm]\dot{m}_{mix} \cdot h_{mix} &= \dot{m}_{HT} \cdot h_{HT} + \dot{m}_{NT} \cdot h_{NT} && \qquad(6).\\[.3cm] \\ \end{aligned}\end{equation} \)Werden die Massenströme durch die Definition aus den Gleichungen 3 und 4 ersetzt, ergibt sich:
\(\\ \begin{equation} \begin{aligned} \dot{m}_{mix} \cdot h_{mix} &= \alpha \cdot \dot{m}_{mix} \cdot h_{HT} + (1-\alpha) \cdot \dot{m}_{mix}\cdot h_{NT} && \qquad(7),\\[.3cm] h_{mix} &= \alpha \cdot h_{HT} + (1-\alpha) \cdot h_{NT} && \qquad(8).\\[.3cm] \\ \end{aligned}\end{equation} \)Die Kürzung um die als konstant angenommene Wärmekapazität und die Umstellung nach \( \alpha \) werden durchgeführt:
\( \begin{equation} \begin{aligned} T_{mix} \cdot c_{p\ mix} &= \alpha \cdot T_{HT} \cdot c_{p\ HT}+ (1-\alpha) \cdot T_{NT} \cdot c_{p\ NT}&& \qquad(9),\\[.3cm] T_{mix} &= \alpha \cdot T_{HT} + (1-\alpha) \cdot T_{NT} && \qquad(10),\\[.3cm] T_{mix} &= \alpha \cdot (T_{HT} – T_{NT}) + T_{NT} && \qquad(11),\\[.3cm] \alpha &= \frac{T_{mix}-T_{NT}}{T_{HT}-T_{NT}} && \qquad(12).\\[.3cm] \\ \end{aligned}\end{equation} \)Die erzeugten Wärmemengen werden wie folgt berechnet:
\( \\ \begin{equation} \begin{aligned} \dot{Q}_{NT} &= \dot{m}_{NT} \cdot c_p \cdot (T_{NT} – T_{Ruecklauf}) && \qquad(13),\\[.3cm] \dot{Q}_{NT} &= (1-\alpha) \cdot \dot{m}_{mix} \cdot c_p \cdot (T_{NT} – T_{Ruecklauf}) && \qquad(14),\\[.3cm] \dot{Q}_{HT} &= \dot{m}_{HT} \cdot c_p \cdot (T_{HT} – T_{Ruecklauf}) && \qquad(15),\\[.3cm] \dot{Q}_{HT} &= \alpha \cdot \dot{m}_{mix}\cdot c_p \cdot (T_{HT} – T_{Ruecklauf}) && \qquad(16),\\[.3cm] \frac{\dot{Q}_{HT}}{\dot{Q}_{NT}} &= \frac{\alpha}{1-\alpha} \cdot \frac{T_{HT}-T_{Ruecklauf}}{T_{NT}-T_{Ruecklauf}}&& \qquad(17).\\[.3cm] \\ \end{aligned}\end{equation} \)Die Gleichungen 12 und 17 sind entscheidend, denn sie bilden die Rechenvorschrift für das Wärmemengenverhältnis zur Einhaltung der minimalen Mischungstemperatur (Solltemperatur).
Mit den aufgeführten Gleichungen wurde für das erste Beispiel der konstante Faktor \( c \) berechnet.
In der Benutzerdefinierten Steuerung sind die Gleichung 12 zur Berechnung einer hier eingeführten Hilfsgröße \( \alpha \) hinterlegt und die Konstante \( c \) definiert:
\( \begin{equation} \begin{aligned} \alpha &= \frac{T_{mix}-T_{NT}}{T_{HT}-T_{NT}} && \qquad(12),\\[.3cm]c &= \frac{\alpha}{1-\alpha} \cdot \frac{T_{HT}-T_{Ruecklauf}}{T_{NT}-T_{Ruecklauf}} && \qquad(18).\\[.3cm] \\ \end{aligned}\end{equation} \)
Da die Mischungstemperatur nur mindestens und nicht genau erreicht werden soll, wurde in der Benutzerdefinierten Steuerung anstelle der Gleichung 17 der Herleitung die folgende Ungleichung formuliert:
\( \begin{equation} \begin{aligned} \frac{\dot{Q}_{HT}}{\dot{Q}_{NT}} &\ge \frac{\alpha}{1-\alpha} \cdot \frac{T_{HT}-T_{Ruecklauf}}{T_{NT}-T_{Ruecklauf}} && \qquad(19).\\[.3cm] \\ \end{aligned}\end{equation} \)Es gilt entsprechend der Gleichung 1:
\( \begin{equation} \begin{aligned} \frac{\dot{Q}_{HT}}{\dot{Q}_{NT}} &\ge c && \qquad(20).\\[.3cm] \\ \end{aligned}\end{equation} \)Diese Vorgabe lässt sich individuell ändern.
Hochtemperatur > Solltemperatur > Niedertemperatur.
Fälle, in denen diese Bedingung nicht erfüllt ist, müssen in der Steuerung mit if-else-Konstruktionen und jeweils eigenen Rechenvorschriften abgedeckt werden.
Im Tutorial sind die folgenden drei Fallunterscheidungen als if-else-Konstruktionen in der Benutzerdefinierten Steuerung implementiert.
Niedertemperatur gleich Hochtemperatur
Wenn die Nieder- und die Hochtemperatur denselben Wert annehmen, würde \( \alpha \) (in Gleichung 12) gegen unendlich streben. Da dies rechnerisch nicht möglich ist, wird die Schranke aufgehoben, indem für diesen Fall \( \alpha = 0 \) gesetzt wird.
Hochtemperatur gleich Solltemperatur
Wenn die Hochtemperatur gleich der Solltemperatur ist, würde \( \alpha \) (in Gleichung 12) den Wert 1 annehmen, und \( c \) (in Gleichung 18) gegen unendlich streben. Da dies rechnerisch nicht möglich ist, wird in diesem Fall \( \alpha = 0 \) gesetzt. Eine zweite Hilfsgröße \( \beta \) wird eingeführt, welche in diesem Fall die Niedertemperaturwärmeproduktion verbietet:
\(\begin{equation} \begin{aligned} \\ Q_{NT} \le \beta \cdot 1000 && \qquad(21).\\[.3cm] \end{aligned}\end{equation} \)
Der Wert 1000 ist das sogenannte Big M und muss größer gewählt werden, als die maximal mögliche Wärmemenge.
Hochtemperatur kleiner Solltemperatur
Wenn die Hochtemperatur kleiner als die Solltemperatur ist, ändert sich die Bedingung in die entgegengesetzte Richtung. Die Systematik zur Berechnung von \( \alpha \) und \( c \) wurde deshalb mit vertauschten Rollen für die Nieder- und die Hochtemperatur angewendet. Die resultierenden Größen wurden \( \alpha_{2} \) und \( c_{2} \) genannt. Diese Schranken sind ebenfalls in die Komponente Benutzerdefinierte Steuerung implementiert.
Strukturell andere Energiesysteme
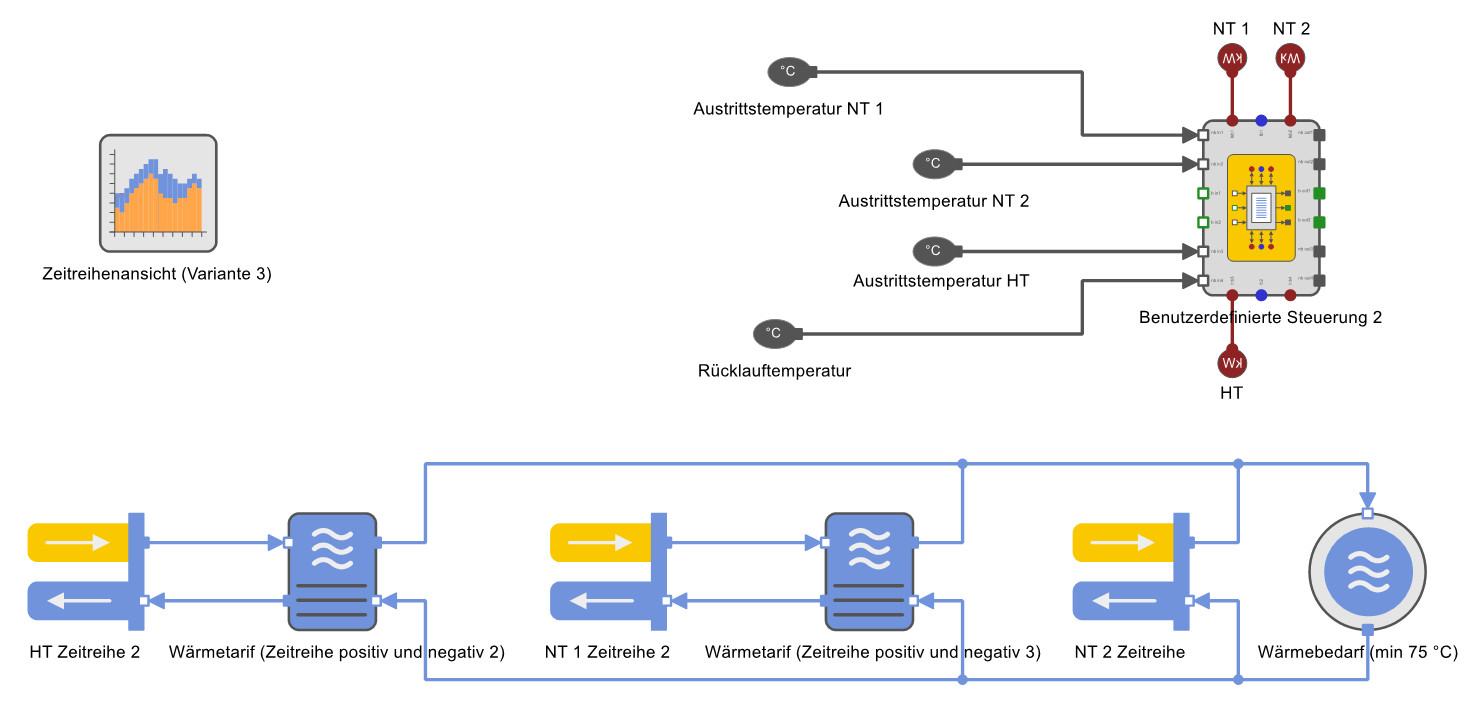
Die gezeigte Methode eignet sich für den oben beschriebenen Anwendungsfall. Darüber hinaus können die Berechnungen erweitert werden. Im Modell des folgenden Schemas (aus dem Simulationsknoten HT-, NT-1- und NT-2-Wärmeerzeugung mit variierender Vorlauftemperatur im Tutorial) werden die Schranken für drei Wärmeerzeuger berechnet.
Die Berechnung erfolgt wie oben, nur anhand der grundlegenden Gleichungen der Thermodynamik. Aus den Mischungsgleichungen werden Randbedingungen für das MILP-Problem formuliert. Für drei Erzeuger lassen sich zwei Bedingungen ableiten:
\( \begin{equation} \begin{aligned} \dot{Q}_{HT\ Teil\ 1} &\ge c_1 \cdot \dot{Q}_{NT\ 1}&& \qquad(22),\\[.3cm] \dot{Q}_{HT\ Teil\ 2} &\ge c_2 \cdot \dot{Q}_{NT\ 2} && \qquad(23),\\[.3cm] \dot{Q}_{HT\ Teil\ 1} + \dot{Q}_{HT\ Teil\ 2} &= \dot{Q}_{HT} && \qquad(24).\\[.3cm] \\ \end{aligned}\end{equation} \)Die Konstanten \( c1 \) und \( c2 \) berechnen sich auf die gleiche Weise wie oben angegeben. Voraussetzung ist, dass die Temperaturen beider Niedertemperaturversorger unter denen der Hochtemperaturversorger liegen. Sonst müssen wie oben mehrere Fallunterscheidungen getroffen werden. Für andere Fälle, wie z. B. variierende Austritts- oder Solltemperatur, müssen diese Berechnungen individuell aufgestellt werden. Dieser Artikel kann nicht alle existierenden Fälle abdecken. Er zeigt nur bespielhaft, wie sich solche Schranken mit den grundlegenden thermodynamischen Gleichungen berechnen lassen.