Cookie Notice

This website uses cookies to ensure you get the best experience on our website. By using this site you agree to the use of cookies. We also use Google Analytics for statistical purposes. By selecting "Accept" you agree to the use of cookies by the Google web analysis service. Learn more about our Data Protection Policies.
Coincidence Factor

Coincidence Factor

Navigation:

Consider the Coincidence Factor in the Supply System

A coincidence factor is not entered directly in TOP-Energy to calculate the demands. The following procedure has proven to be useful to nevertheless take a simultaneity factor into account in TOP-Energy.

The Coincidence Factor

The coincidence factor is used for the appropriate dimensioning of a supply system. It specifies which share of the maximum total demand in a supply system is to be covered simultaneously at a point in time. The factor is based on empirical findings (estimation) and decisions made.\(\)

Example

Because the demand peaks do not occur simultaneously, supplying a street with 10 houses, each of which has a heat demand with a peak load (peak demand load) of 15 kW, does not in practice require a maximum capacity of 150 kW to be provided, but only 105 kW with a coincidence factor of 0.7. The peak load draw is calculated as follows:

\begin{equation} \begin{aligned} \text{Coincidence Factor } \cdot \text{Total Demand} &= \text{Peak Load Draw} \\  0.7 \cdot 10 \cdot 15 \ \text{kW} &= 105 \ \text{kW} \end{aligned}\end{equation}

Scaling Load Profiles

To process this information in TOP-Energy, it may be necessary to scale a single load profile time series. The integral value of the demand should be preserved, only the peak demand should be reduced according to the coincidence factor. This problem cannot be solved unambiguously, and there are no standard procedures for it. In the context of TOP-Energy, the following simple iterative procedure has proven effective, which is demonstrated here using Tutorial 4 as an example:

  • In the Properties of the time series, find the Integral and the Maximum values of the demand (in the example 264.62 MWh Integral and 119.50 kW Maximum).
  • Open the time series in the ETA.
  • Scale the time series with the method Change values -> Scale by the integral value corresponding to the multiple of the Integral value of the single time series (e.g., 10 * 264.62 MWh).
  • Calculate the peak load draw according to the formula given above as the product of the coincidence factor and the multiple of the maximum demand of the single time series (in the example: 0.7 * 10 * 119.50 kW=836.5 kW).
  • Filter the time series with the method Filter time series -> Filter values -> greater than the calculated maximum value (in the example 836.5 kW) and Replace the filtered out values with the same value.
  • The integral of the new time series has now decreased (in the example to 2611 MWh). Therefore, repeat the steps of scaling by integral value and filtering and replacing by peak load once. In the example, the desired maximum of 836.5 kW and the integral value of 2642 MWh result after only one repetition.

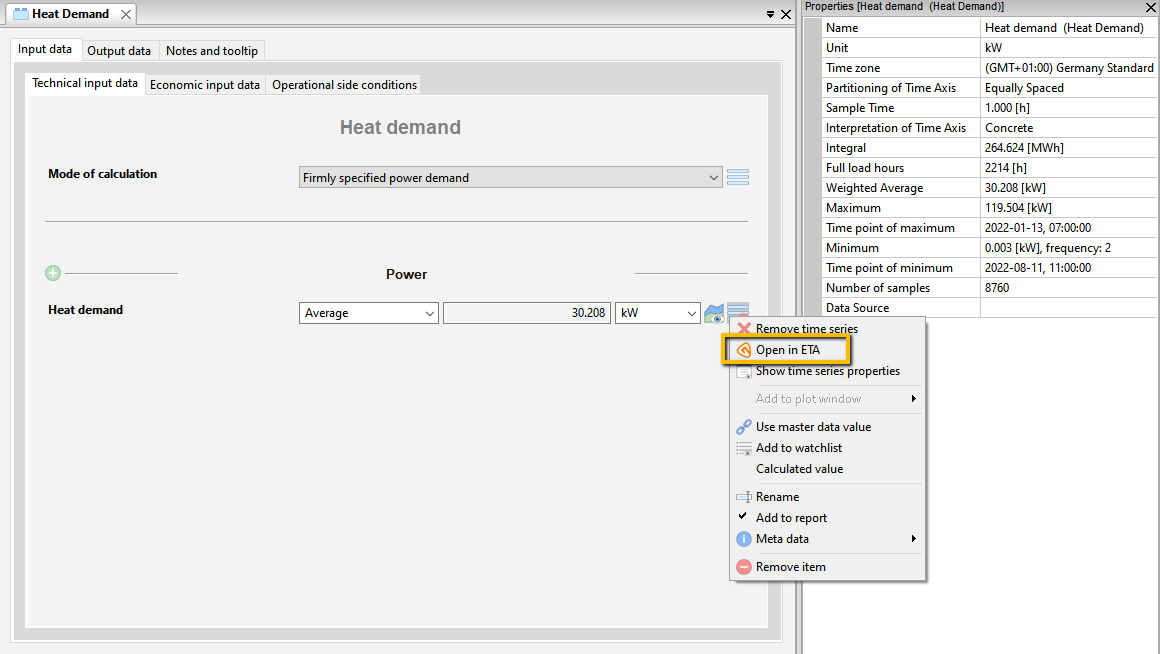
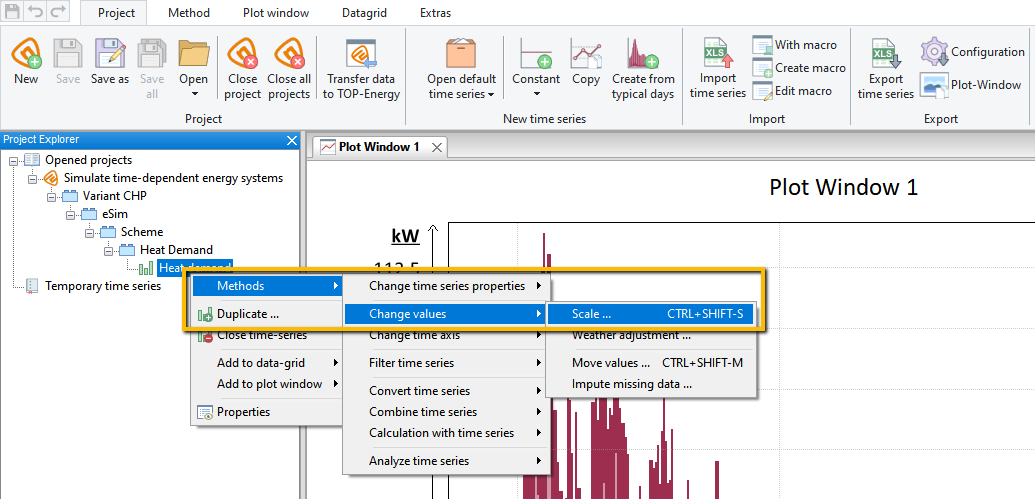
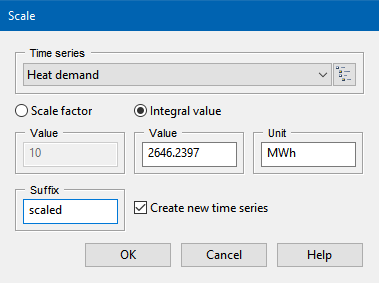
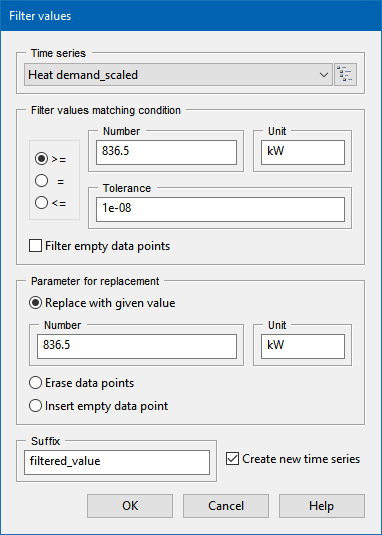
This procedure will give you the correct integral value and the correct load draw. A problem with this procedure is correctly estimating the frequency of occurrence of the maximum load, but this should not have much effect on the design and annual cost of the energy systems.

Back To Top