Consider the Coincidence Factor in the Supply System
A coincidence factor is not entered directly in TOP-Energy to calculate the demands. The following procedure has proven to be useful to nevertheless take a simultaneity factor into account in TOP-Energy.
The Coincidence Factor
The coincidence factor is used for the appropriate dimensioning of a supply system. It specifies which share of the maximum total demand in a supply system is to be covered simultaneously at a point in time. The factor is based on empirical findings (estimation) and decisions made.\(\)
Because the demand peaks do not occur simultaneously, supplying a street with 10 houses, each of which has a heat demand with a peak load (peak demand load) of 15 kW, does not in practice require a maximum capacity of 150 kW to be provided, but only 105 kW with a coincidence factor of 0.7. The peak load draw is calculated as follows:
\begin{equation} \begin{aligned} \text{Coincidence Factor } \cdot \text{Total Demand} &= \text{Peak Load Draw} \\ 0.7 \cdot 10 \cdot 15 \ \text{kW} &= 105 \ \text{kW} \end{aligned}\end{equation}
Scaling Load Profiles
To process this information in TOP-Energy, it may be necessary to scale a single load profile time series. The integral value of the demand should be preserved, only the peak demand should be reduced according to the coincidence factor. This problem cannot be solved unambiguously, and there are no standard procedures for it. In the context of TOP-Energy, the following simple iterative procedure has proven effective, which is demonstrated here using Tutorial 4 as an example:

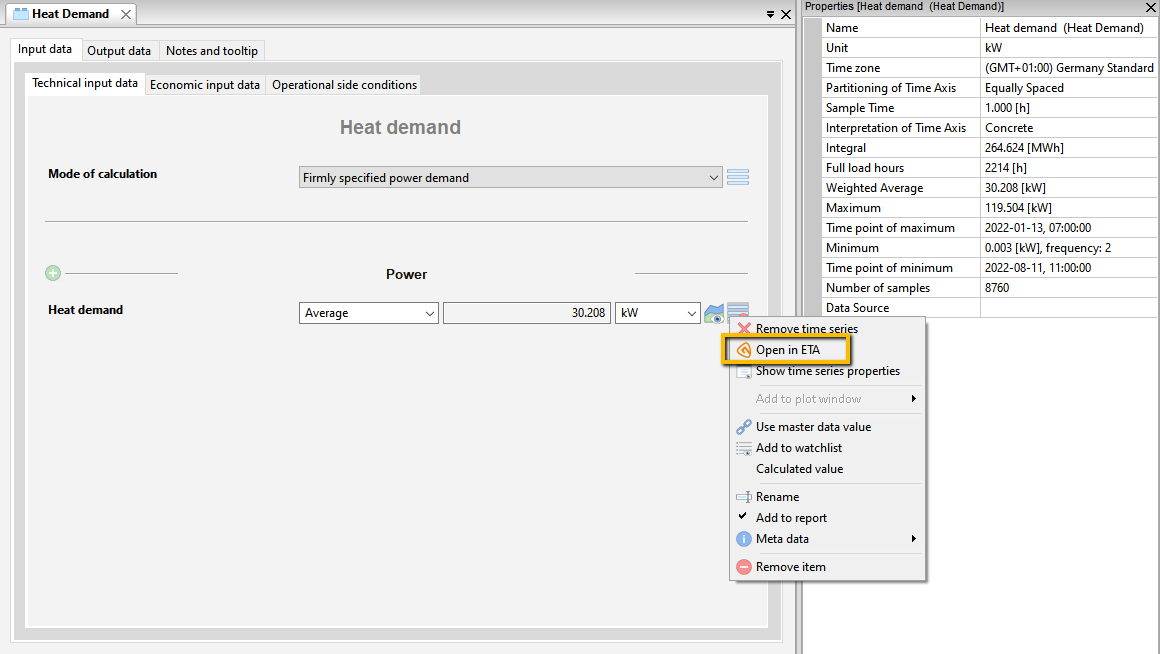
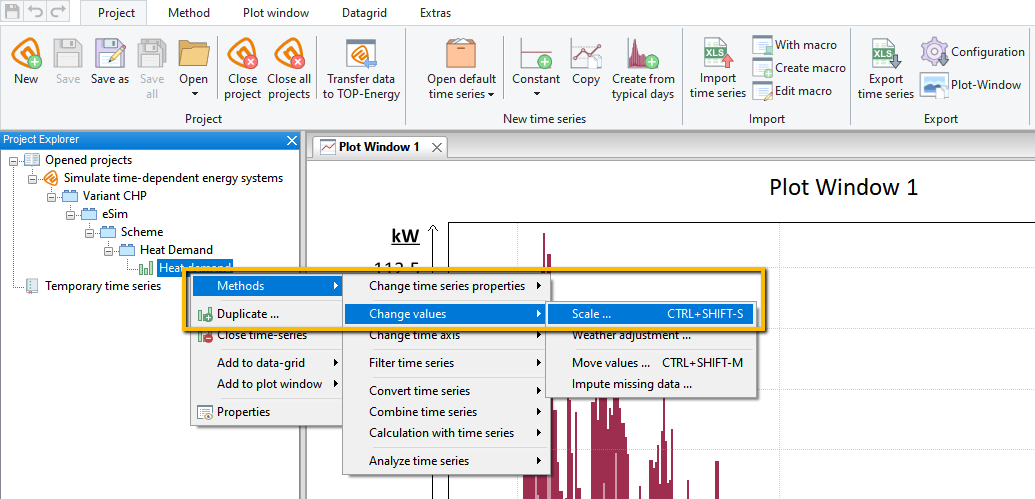
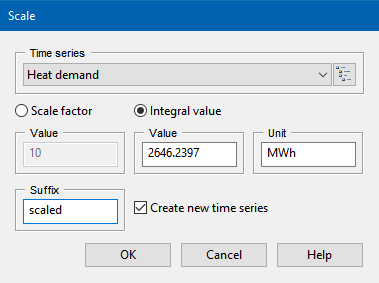
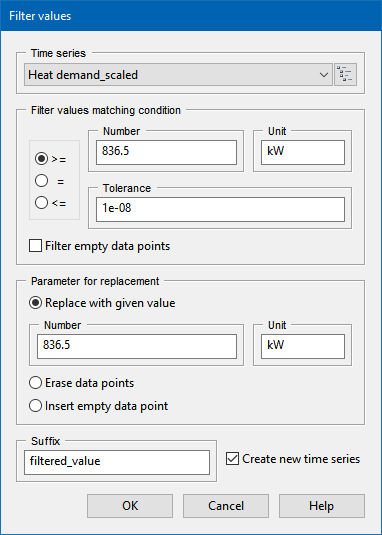
This procedure will give you the correct integral value and the correct load draw. A problem with this procedure is correctly estimating the frequency of occurrence of the maximum load, but this should not have much effect on the design and annual cost of the energy systems.
